【LIQUID】使用鎖相放大器和相位計進行相位檢測—操作原理指南

使用鎖相放大器和相位計進行相位檢測

操作原理指南

使用Moku鎖相放大器和相位計進行開環和閉環相位檢測的選擇指南。

高精確度及高靈敏度相位檢測在眾多測試量測場域都至關重要。例如，測量電流和電壓之間的相移可以顯示設備或元件的複數阻抗。可以通過光學干涉儀的控制臂和測量臂之間的相移來量測極小的位移。Liquid Instruments的Moku設備可以提供兩種檢測射頻訊號相位的儀器：鎖相放大器和數位相位測量儀。 在本應用說明中，將介紹這兩個儀器的工作原理，並為不同的應用場域提供儀器選擇指南。

介紹

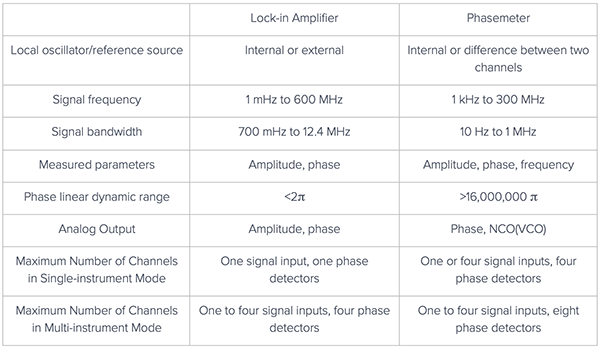
鎖相放大器和相位計（數位相位測量儀）是兩種常用於從振蕩訊號中擷取相位資訊的儀器。 鎖相放大器可以被視為開環相位檢測器。相位是由本地振蕩器、混頻器和低通濾波器直接計算出來的。相比之下，相位計則採用數位鎖相環（PLL）作為其相位檢測器，使用一個回饋訊號來即時調節本地振蕩器的頻率。這可以被視為一種閉環相位檢測方法。

介紹這兩種儀器之前，先來總結一下Moku：Pro鎖相放大器和相位計（用於相位檢測）的區別。請注意，本表中的參數規格是基於Moku：Pro的。

工作原理

鎖相放大器原理

如圖1所示，鎖相放大器有三個關鍵組成部分：一個本機振蕩器、一個混頻器和一個低通濾波器。

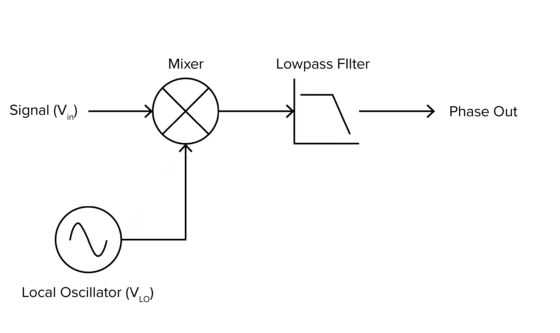
圖1：鎖相放大器的簡化原理圖

輸入訊號V_in和本機振蕩器V_LO可以用正弦和餘弦函數來描述：

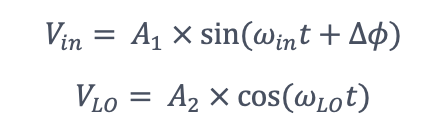
A₁和A₂代表振蕩器的振幅。ω_in和ω_LO代表輸入和本機振蕩器的頻率。∆φ表示輸入訊號和本機振蕩器之間的相位角差。混頻器的輸出V_mixer是輸入和本機振蕩器的產生的。

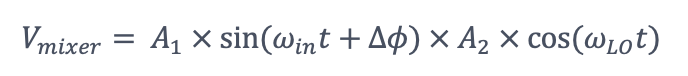
應用三角函數示意

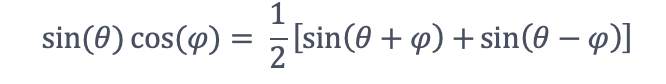
假設 ω_LO ≅ ω_in= ω， V_mixer可寫為

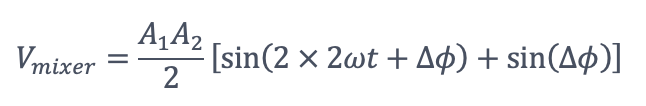
低通濾波器過濾掉了高頻率分量sin⁡(2×2ωt+∆ϕ)。假設輸入訊號和本機振蕩器的振幅是固定的，輸出訊號V_out可以表示為

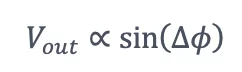
在此有幾個需要注意的地方：單相鎖相放大器的輸出與sin（∆φ）成正比，而不是與成正比。這大大限制了相位檢測的線性動態範圍，因為正弦函數是一個週期性的函數，它只在一個非常小的範圍內提供（近乎）線性回應。 另外，任何振幅的波動都可能引起一些系統誤差。Liquid Instruments的Moku鎖相放大器提供了雙相解調的選項，可有效地區分了來自振幅和相位對輸出的影響，但線性動態範圍仍然限制在2π以內。另一方面，鎖相放大器的數位訊號處理（DSP）比相位計簡單得多。這使鎖相放大器能夠以更快的速率處理數據，從而提供更寬的解調頻寬。使用者也可從外部設備輸入一個本機振蕩器作為參考，以直接測量兩個振蕩器之間的相對相位差。鎖相放大器的開環特性確保儀器能夠提供有效即時的回應，不容易受訊號突變或損失造成的影響。因此，用戶可使用鎖相放大器測量接近或處於輸入本底雜訊的訊號。

相位計/PLL 原理

相位計的核心相位檢測單元是一個鎖相環（PLL）。相位計的基本測量原理是將一個內部振蕩器鎖定在輸入訊號上，然後從內部振蕩器的已知相位推斷出輸入訊號的相位。圖2顯示了PLL的運作原理。鎖相環的運作原理與鎖相放大器非常類似，但有兩個重要的區別：1）本機振蕩器被一個壓控振蕩器（VCO）所取代；2）低通濾波器的輸出回饋形成一個閉環。

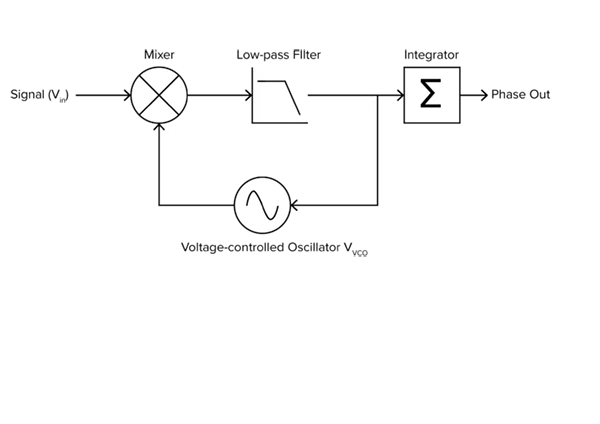
圖2：鎖相環的簡化原理圖
VCO的輸出 V_VCO可以表述為

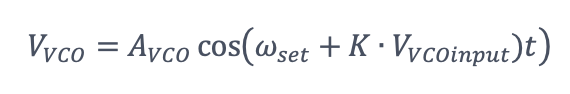
ω_set是VCO的設定/中心頻率。K是VCO的靈敏度，V_VCOinput 是VCO的輸入。A_VCO是VCO的振幅。K和A_VCO在正常工作時都保持不變。在不深入瞭解閉環控制理論的情況下，這種設定試圖保持輸入訊號V_in和V_VCO之間的暫態頻率差為零。 因此：

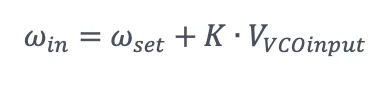
由於ω_set和K都是基於已知的儀器設定，輸入的頻率可以根據V_VCOinput來計算。同時，ω_set在時間t的累積相位可以表示為

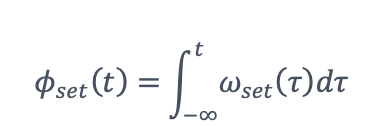
輸入訊號的累積相位可以用來近似表示。這裡我們把K∙V_vcoinput項定義為ω_diff。

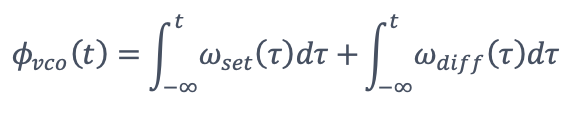
因此，輸入訊號和參考訊號（振蕩器在設定的頻率下）之間的累積相位差可以通過推測計算環路的頻率差/誤差訊號積分擷取。

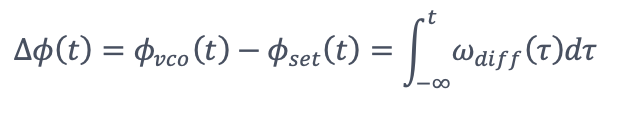
這種方法為相位檢測提供了一個原生的相位解包支援，使輸出與相位差呈線性關係。輸入訊號的暫態頻率也通過進行測量。此外，相位計有一個內置的二級振蕩器來計算輸入訊號的振幅，類似於一個雙相鎖相放大器。除了來自環外積分器的相位，相位計的輸出可以被設定為直接從數控振蕩器（NCO; 它可以被認為是數位的VCO）產生輸入訊號的正弦鎖相副本，具有任意的振幅和可調相位。另一方面，輸入和NCO之間的穩定鎖定是PLL正常運行所必須的，不連續的輸入可能會導致測量中斷。 由於這個原因，PLL在非常低的頻率上保持穩定的鎖定更具挑戰性，相位計對比於鎖相放大器在低載波頻率邊界更受限制，因此不建議用於測量接近輸入本底雜訊的訊號。

應用中考量因素和演示

在本節中，我們將透過演示討論在對Moku鎖相放大器和相位計之間進行選擇時的一些實際注意事項。

相位檢測的線性動態範圍

鎖相放大器和相位計的關鍵區別之一是相位檢測的線性動態範圍。單相鎖相放大器的相位線性動態範圍小於π，雙相鎖相放大器則將這一極限推至2π。理論上，相位表可以追蹤無限的相位變化。在實踐中，實際檢測範圍受用於表示相位的數位位長度的限制，在Moku：Pro上大約是16,000,000π。

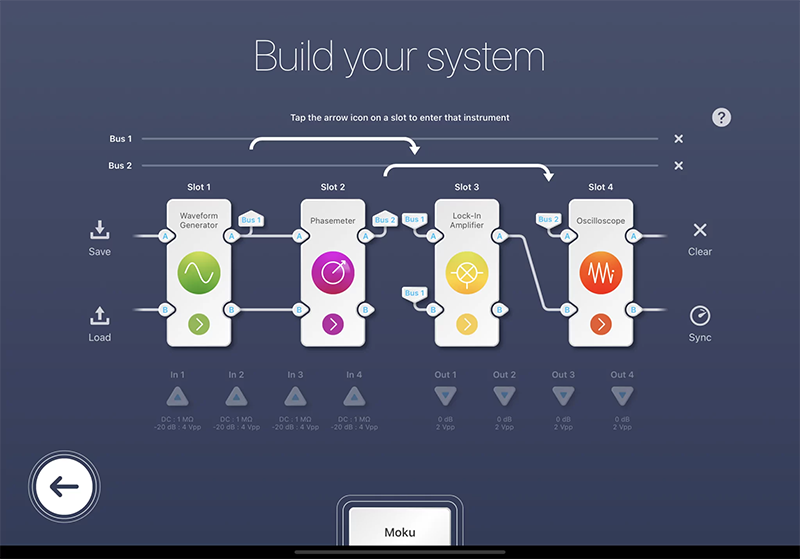
在這個演示中，透過多儀器模式（MIM）。同時，開啟波形產生器、鎖相放大器、相位計和示波器功能。一個10MHz的相位調製訊號以單相和雙相模式輸入Moku：Pro的鎖相放大器和相位計。相位檢測的輸出通過示波器進行記錄。

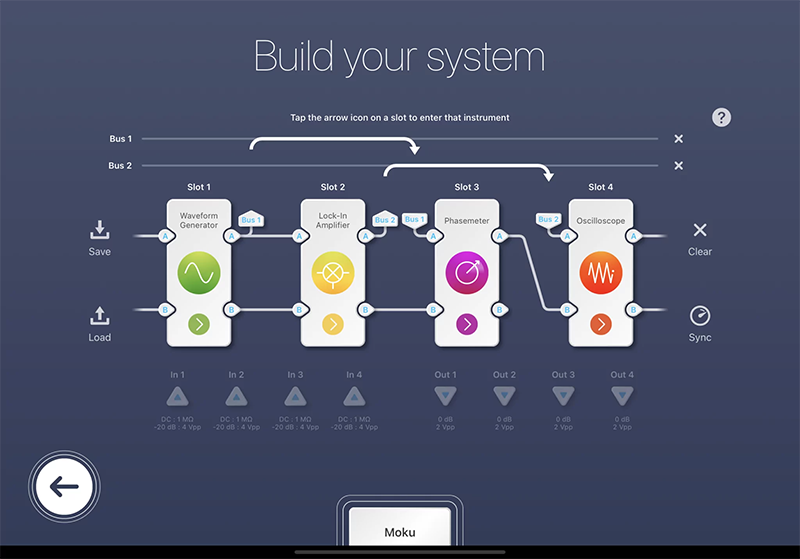
圖3：Moku：Pro上的MIM設置，用於測試不同相位檢測器的線性動態範圍。

標準化的相位輸出（作為模擬訊號）繪製成圖4中相移的函數。從圖4(a)來看，雙相解調模式下的相位表和鎖相放大器都在360°範圍內提供線性相位響應。單相模式下的鎖相放大器只提供了90°內的近線性響應。 雙相解調器將相位包裹在±180°，而PLL在整個720°的相位移動範圍內持續線性輸出（圖4(b)）。

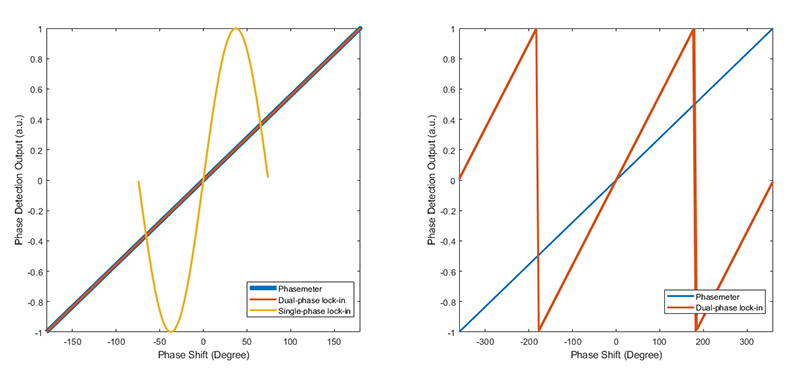
圖4：相位計、鎖相放大器在單相和雙相模式下的輸出與 (a) 360° 和(b) 720° 的相移關係

與鎖相放大器相比，相位計的另一個主要優勢是相位誤差訊號可以被解開，並在PLL內累積。這使得閉合環路可以被鎖定，即使在多雜訊的系統中使用慢速執行器也是如此。鎖定放大器可以在慢速執行器對輸入作出反應之前將相位誤差訊號包裹起來。

使用不穩定參考進行測量

對於測量兩個振蕩訊號之間的相對相移的應用，鎖相放大器提供了一個更直接的檢測方式。 用戶可以透過Moku鎖相放大器直接輸入一個參考訊號作為本機振蕩器來解調兩個訊號間的相位差。相位計的操作則需要一個板載振蕩器作為絕對頻率參考，因此檢測的相位為訊號與板載振蕩器的相位差。

在這個演示中，一個頻率調製（FM）的不穩定訊號被送入鎖相放大器作為訊號和參考，而相位表作為訊號，如圖5(a)所示。 在圖5(b)中，調頻引起的相位波動只在相位表（紅色）上觀察到，鎖相放大器的輸出保持不變（藍色）。 鎖相放大器的輸出為調頻訊號與其本身的即時相位差，因此是固定沒有波動的。 相位表檢測的結果為調頻訊號與板載振蕩器間的即時相位差，因此檢測到的是數據的載波。

(a)

(b)

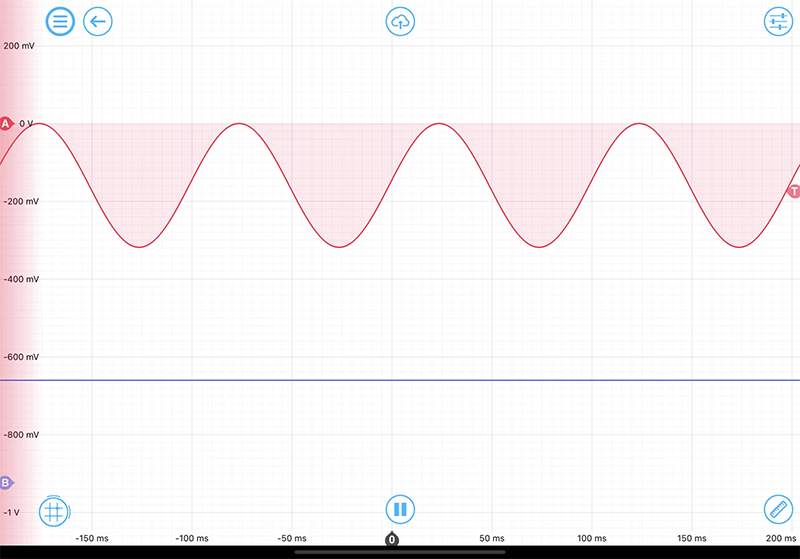
圖5：(a)一個調頻調製訊號被接入到相位表的訊號輸入通道，以及鎖相放大器的訊號和參考輸入。
(b)示波器上的相位表（紅色）和鎖相放大器（藍色）的輸出。

在此有兩種方法可以用相位計測量兩個振蕩器之間的相對相位差。 1）兩個輸入訊號之間的相位差可以通過∆φ₁-∆φ₂，來計算，其中∆φ_1,2 代表輸入到一個共同參考的相位差。 圖6中顯示了一對具有180°相移的鎖相正弦波使用相位計內置的數據記錄監測用來記錄∆φ₁（紅色）、∆φ₂（藍色）和 ∆φ₁-∆φ₂（橙色）。 在兩個輸入通道上可以觀察到穩定的相位漂移，但運算通道提供了輸入之間的正確相位差。

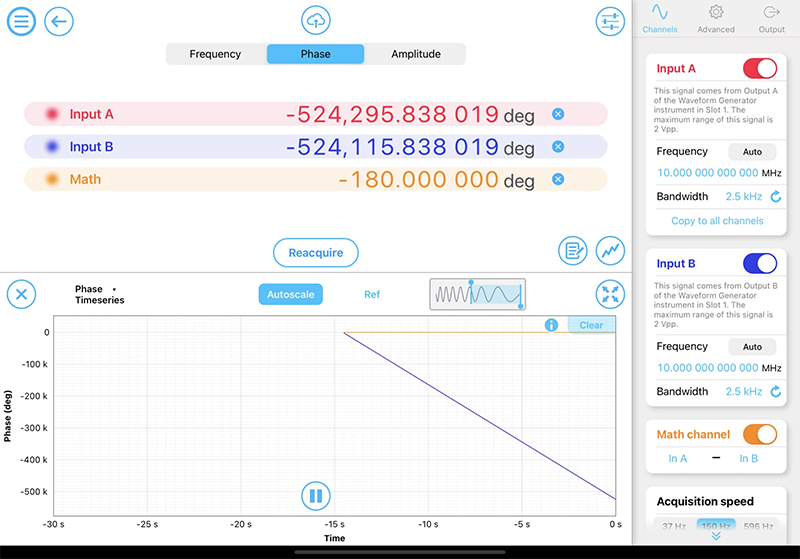
圖6：一對具有180°相移的正弦波被發送到相位計中。∆φ繪製在運算通道中。

2）Moku：Lab和Moku：Pro的主時鐘可以通過一個10 MHz的參考訊號進行同步。如果參考振蕩器可以與10 MHz同步，這就使得Moku：Pro上NCO的時基與參考相同。然而，時基同步並不能擷取到參考NCO的任何參數調整（比如參考源是有目的地進行頻率調製的）。另外，用於擷取10MHz參考的PLL可能會給系統帶來額外的雜訊。除非需要透過類比通道輸出即時差異，否則不推薦使用這種方法。

測量接近本地雜訊的訊號

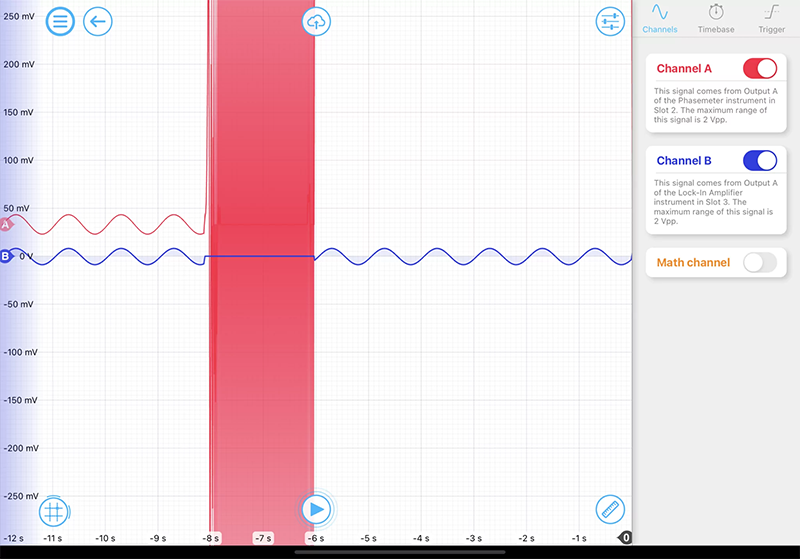
相位計要求輸入訊號和本地振蕩器之間有穩定的鎖定。Moku相位計有幾個內建的安全機制來防止意外的變化對測試造成影響。例如，當鎖定遺失時，「飛輪」選項會自動將環路保持在最後的已知狀態。另一方面，鎖相放大器的輸出在任何時候都是確定的。為了演示這一效果，一個正弦相位調製的訊號被同時輸入到鎖相放大器和相位計上。然後，輸入訊號被切斷約兩秒鐘，再打開。兩個相位檢測器的輸出通過示波器進行記錄。從圖7中可以看出，重新連接訊號後，相位計的輸出（紅色）快速漂移。鎖相放大器的輸出（藍色）在訊號斷開時保持在0，之後立即恢復到預期值。

總結

Liquid Instruments的Moku：Lab和Moku：Pro的相位計和鎖相放大器是為靈敏的相位檢測應用提供的兩種軟體定義的儀器功能。相位計的閉環方法提供了特殊的線性動態範圍。同時，提供輸入的頻率、相位和振幅資訊。鎖相放大器演算法相對簡單，可以提供更快的響應速度，並且輸出結果更容易預測。透過多儀器模式，這些儀器可以在單個FPGA芯片上並行部署。在四個輸入通道上最多可以部署八個基於PLL的相位檢測器。Moku:Pro是多通道相位檢測和鎖相環應用的理想解決方案。

參考文獻 

[1] Shaddock, D., Ware, B., Halverson, P. G., Spero, R. E., & Klipstein, B. (2006, November). Overview of the LISA Phasemeter. In AIP conference proceedings (Vol. 873, No. 1, pp. 654-660). American Institute of Physics.

[2] Roberts, L. E. (2016). Internally sensed optical phased arrays.